Summary
We present the Distributed and Unified Numerics Environment (DUNE). It is an open source C++ software framework for the parallel solution of partial differential equations with grid-based methods. It allows users to rapidly build their own custom parallel simulation software using provided building blocks.
Unlike other frameworks it is designed for parallel computations from the ground up. It is not built around fixed data structures, but represents a fine grained interface to several supported grid managers (simplicial, structured, unstructured, adaptive, …), and solvers. Algorithms based on the interface can switch between different components, and approaches without loosing performance due to generic programming techniques.
We present a parallel application realized with DUNE and show its scalability on supercomputers with up to nearly 300,000 cores and 150 billion unknowns.
Introduction
Most simulation software is built around around fixed components, e.g. a specific mesh manager, or a specific solver package. This not only limits it to a specific narrow application area but also makes it hard to profit from new algorithmic improvements of current research. With the advent of high performance computing for the masses via cloud computing, multi-core machines in the offices (and even smart phones), and affordable accelerators by various vendors this has become a critical issue for many simulation software packages. Often these have been developed for single core machines and are now hard and expensive to port to modern high performance computing platforms.
On the other hand at least in academia there has been intensive research of algorithms for high performance computing for several decades. Often this has been done in a proof-a-concept kind of way for producing fast research results while neglecting software engineering issues like modularity and code reuse. But there are several exceptions to this rule like the "Portable, Extensible Toolkit for Scientific Computation" (PETSc) [14][1][2], Deal II [9][3], and last but not least the "Distributed and Unified Numerics Environment" (DUNE) [11][6][5][7]. All of these are open source packages for solving partial differential equations that have been developed as parallel software from the start and have since then been continuously adapted the most current high performance computing platforms. They all have shown to scale to thousands and sometimes even hundreds of thousand of cores.
Among them DUNE stands out due to the following facts: - Distributed development: DUNE was started in 2002 as a common effort by various institutions with various application backgrounds. This ensures that the software is not limited to a specific application area. Today the core development team stems from seven institutions, both academia and industry, in 3 European countries. - Modularity: DUNE is not a monolithic software but divided into several modules, each for its own purpose. It allows users to build their own custom purpose efficient simulator by choosing the right module and backends. - Exascale: DUNE is part of the German priority program "Software for Exascale Computing" (SPPEXA) [15] which aims to ensure scalability beyond tomorrows millions of processing units. - Third party frameworks: There exist several third party simulation packages for special purposes based upon DUNE, such as the "Open Porous Media Initiative" (OPM) [13], "DUNE for Multi-{Phase, Component, Scale, Physics, …}" (DUMUX) [10], and others. - Professional scientific support, training, and contract work for extensions are available for "Dr. Blatt - HPC-Simulation-Software & Services".
The Distributed and Unified Numerics Environment
DUNE, the "Distributed and Unified Numerics Environment" [11][6][5][7] is a modular software toolbox for solving partial differential equations written in C++. It is licensed under the GNU General Public Licence (GPL) version 2 with the so-called "runtime exception" that allows compiling and linking it together with proprietary software.
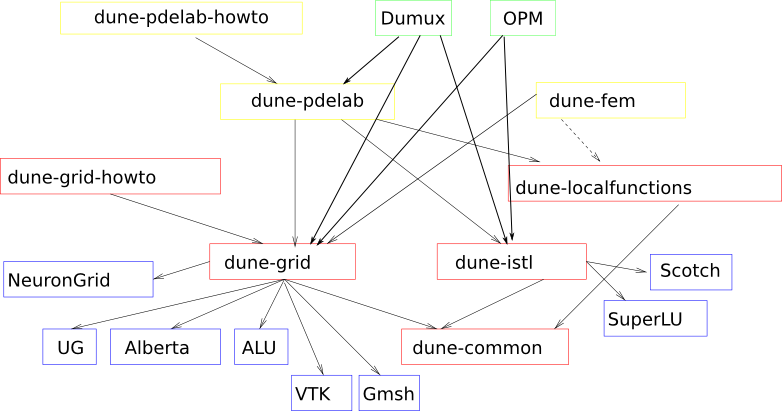
DUNE is supposed to be a template library for all software components required for the numerical solution of partial differential equations. Figure 14 shows the high level design. It consists of several core modules (red boxes), other modules provided by core DUNE community (yellow boxes), and other third party DUNE modules (green boxes). Each module suits its own special purpose. User code will access geometries, grids, sparse linear solvers, etc. through the abstract interfaces. Many specialized implementations of one interface are possible and particular implementations are selected at compile time. This concept allows easy incorporation of existing codes as well as coupling of different codes. To prevent reinventing the wheel DUNE also uses legacy codes (blue boxes).
The Parallel Grid Interface (dune-grid)
The abstract mesh interface provided in the module dune-grid supports finite element grids with the following properties: - Grids with elements of arbitrary dimension embedded in a space with the same or higher dimension can be described. - Grids may have elements of arbitrary shape (there is a way to define reference elements) and arbitrary transformation from the reference element to the actual element. - Grids may be nonconforming, i.e. the intersection of two elements need not be a common vertex, edge or face. - Local refinement is always nested. I.e. every fine grid element results from subdivision of exactly one coarse grid element. - Grids may be partitioned into overlapping sub grids for parallel processing.
Several mesh objects of different type can be instantiated in one executable in order to couple problems on different grids.
Each grid provides mappings of classes of entities onto consecutive indices. This allows the storage of user data outside of the mesh in contiguous memory location (e.g. arrays or ISTL vectors), e.g. for efficient usage of the cache in the fast linear algebra. During grid adaptions the grid entities can be identified via unique ids to move data from one grid representation to the other.
Parallel grids in the DUNE interface use an overlapping domain decomposition, i.e. each process does not only store its partition of the mesh cells but also ghost and/or overlap cells. In Figure 25 we illustrate the cells stored on one process of a parallel overlapping grid. The red cells are part of the partitioning of the process. In DUNE these form the so-called owner partition. The process is responsible for computing values on it. The green cells are part of the overlap partition. These are cells that are part of the owner partition on other processes. The values associated with these are normally obtained by communication. There do exist other partitions in DUNE omitted here. The grey cells are not stored on the process at all.
To facilitate communication of associated data a DUNE grid also associates a unique global id with each grid entity. This is used together with the partition type in the grids' methods for communicating user data.

The following parallel grid implementations are available - ALU3DGrid: Unstructured tetrahedral and hexahedral meshes, local mesh refinement with hanging nodes, non-overlapping parallel data decomposition, adaptation of the finite element toolbox ALU3d. Available in external module dune-alugrid. - CpGrid: A parallel cornerpoint grid. Available in external module dune-cornerpoint. - UGGrid: Unstructured multi-element meshes in 2 and 3 space dimensions, red-green type local mesh refinement, non-overlapping decomposition for parallel processing, adaptation of the finite element toolbox UG. - YaspGrid: A parallel tensor product grid in n space dimensions.
The Parallel Iterative Solver Library (dune-istl)
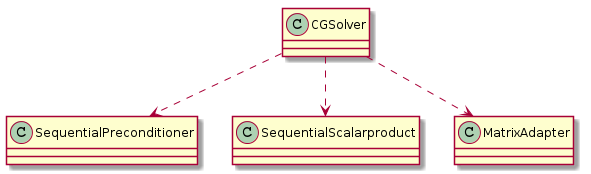
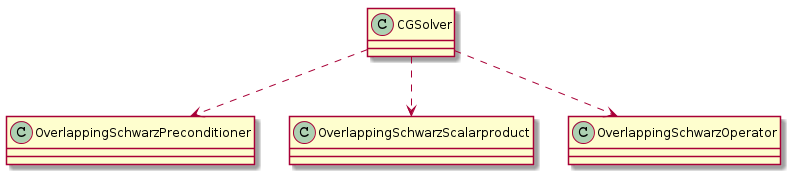
Most of the parallel iterative solver libraries available today use distributed data structures (matrices and vectors) which implicitly know the data distribution and communication patterns. In contrast to this the "Iterative Solver Library" (ISTL) [7][8], available in the DUNE module dune-istl, the information about the data distribution and the communication schemes is kept separate from the linear algebra data structures. This clear separation allows for reusing the efficient sequential components wherever possible and limiting the slow communication steps to a minimum. The information is provided by parallel index sets which can be constructed from the parallel grids of the dune-grid module, or setup manually. This allows to use the parallel iterative solvers independently of the grid interface. Using the index set information a consistency model is imposed onto the building blocks (scalar products, preconditioners, and linear operators) of the iterative solvers (conjugate gradient, stabilized bi-conjugate gradient method, GMRes).
This consistency model allows for easily switching the underlying parallel or sequential programming paradigm. If the user chooses a sequential scalar product, linear operator, and preconditioner (see Figure 33) then the resulting iterative solver is purely sequential without any additional overhead. If he or she chooses matching parallel components (see Figure 34) instead, then is becomes an efficient and scalable parallel solver.
Plug-Code-And-Play for Efficient Parallel Simulators (dune-pdelab)
Dune-pdelab [4] is one of DUNE's discretization modules. It was developed to allow rapid prototyping of simulators. With it the time to develop new discretizations and solvers for systems of PDEs is reduced. It is used for productive simulators as well as for teaching purposes. While the use of dune-grid allows for exchanging the grids used by the simulator, it uses a linear algebra backend that also allows for exchanging the linear algebra packages used (currently: dune-istl and PETSc). The design of dune-pdelab is based on a weighted residual formulation rh of the underlying PDEs:
Find uh ∈ wh + Uh: rh(uh, v) = 0 ∀ v ∈ Vh, where Uh, and Vh are subspaces of finite dimensional test and trial function spaces. rh is linear or nonlinear in the first argument, and always linear in the second one.
It can be mathematically formulated for a large class of partial differential equations. The form can be split into a part defined on the elements, on the facets, and on the boundary.
The anatomy of simulator can be seen from Figure 39. To create a custom simulator the user chooses a grid with the properties needed. Then he or she chooses one of the predefined flexible discrete function spaces. There are instances supporting conforming, and non-conforming discretizations, hp-refinement, and product spaces for systems. If the user needs or wants to implement new discretization schemes or models then he or she can formulate the local grid and time operators needed by the weighted residual from using a local representation of the finite element. The projection onto the global space is done automatically. After choosing the the non-linear, and linear solvers in the backend and possibly a time stepping scheme, the simulator is finished and can be compiled into an efficient program.
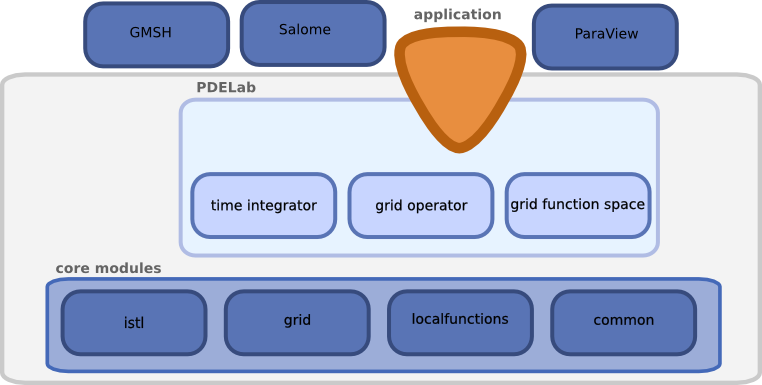
If parallel versions of the grid, grid function spaces, and solvers are chosen then the simulator is parallel at no additional cost.
At least the following applications have been realized with dune-pdelab - Various elliptic, parabolic and hyperbolic model problems. - Higher-order conforming and discontinuous Galerkin finite element methods. - Cell-centered finite volume method. - Mixed finite element method. - Mimetic finite difference method. - Incompressible Navier-Stokes equations. - Two-phase flow. - Multi-phase flow in porous media. - Linear acoustics. - Maxwell's equations.
A Real World Scalability Example from Flow in Porous Media
To show the weak scalability (number of degrees of freedom per process remains constant) of simulators realized with DUNE we present results obtained together with Olaf Ippisch, now professor at the TU Clausthal. For more details see [12].
We simulate the infiltration of a heterogeneous soil starting at hydraulic equilibrium using Richards' equation. The material parameters of the soil were either - homogeneous, scenario homog. - heterogeneous with a heterogeneity which was the same on each compute node, scenario block. - heterogeneous with a structure which was much larger, scenario block.
At the sides we impose no-flux boundary conditions and at the lower boundary a constant potential of zero and at the top a constant flux of 2mm/h. The size of a grid element was 0.01m x 0.01m x 0.01m. We simulated one time step of one hour. During the weak scalability test with 64 x 64 x 128 grid cells per process we increased the domain only in the horizontal direction. The solution is done using a cell-centered finite volume scheme, Newton's method as the nonlinear solver, and dune-istl's non-smoothed algebraic multigrid method as the linear solver. Up to 294 849 processes were used, resulting in 150 billion unknowns.
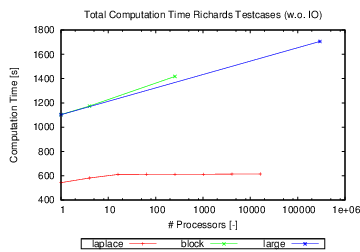
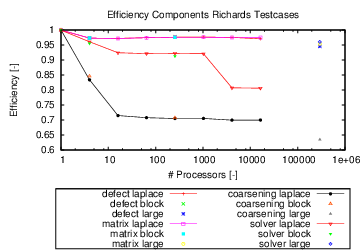
In Figure 58 we show the total computation time without any IO. In Figure 59 we show the efficiency of the various solver components: defect calculation (defect), matrix assembly (matrix), coarsening of the algebraic multigrid (coarsening), and application of the linear solver (solver). We see that most components of the codes scale very well.
Summary and Outlook
In this blog we have described the various components of the Distributed and Unified Numerics Environment. Using it we have shown how open source building blocks can be used to create custom simulators that allow for massively parallel simulations. These scale well for hundreds of thousands of processes and can be used to solver problems with more than 150 billion degrees of freedom. With the ongoing efforts within the European SPPEXA project this scalability will most likely carry over to next generation HPC systems.
References
| [1] | S. Balay, K. Buschelman, V. Eijkhout, W. D. Gropp, D. Kaushik, M. G. Knepley, L. C. McInnes, B. F. Smith, and H Zhang. PETSc users manual. Technical Report ANL-95/11 - Revision 2.1.5, Argonne National Laboratory, 2004. |
| [2] | S. Balay, W. D. Gropp, L. C. McInnes, and B. F. Smith. Efficient management of parallelism in object oriented numerical software libraries. In E. Arge, A. M. Bruaset, and H. P. Langtangen, editors, Modern Software Tools in Scientific Computing, pages 163--202. Birkhäuser Press, 1997. |
| [3] | W. Bangerth, R. Hartmann, and G. Kanschat. deal.II -- a general purpose object oriented finite element library. ACM Trans. Math. Softw., 33(4):24/1--24/27, 2007. [ DOI ] |
| [4] | P. Bastian, F. Heimann, and S. Marnach. Generic implementation of finite element methods in the distributed and unified numerics environment (DUNE). Kybernetika, 46(2):294--315, 2010. |
| [5] | Peter Bastian, Markus Blatt, Andreas Dedner, Christian Engwer, Robert Klöfkorn, Ralf Kornhuber, Mario Ohlberger, and Oliver Sander. A generic grid interface for parallel and adaptive scientific computing. part II: implementation and test in DUNE. Computing, 82(2--3):121--138, 2008. [ DOI ] |
| [6] | Peter Bastian, Markus Blatt, Andreas Dedner, Christian Engwer, Robert Klöfkorn, Mario Ohlberger, and Oliver Sander. A generic grid interface for parallel and adaptive scientific computing. part I: abstract framework. Computing, 82(2--3):103--119, 2008. [ DOI ] |
| [7] | Markus Blatt and Peter Bastian. The iterative solver template library. In Bo Kagström, Erik Elmroth, Jack Dongarra, and Jerzy Waśniewski, editors, Applied Parallel Computing. State of the Art in Scientific Computing, volume 4699 of Lecture Notes in Computer Science, pages 666--675. Springer, 2007. [ DOI ] |
| [8] | Markus Blatt and Peter Bastian. On the generic parallelisation of iterative solvers for the finite element method. Int. J. Comput. Sci. Engrg., 4(1):56--69, 2008. [ DOI ] |
| [9] | deal.II. http://www.dealii.org/. |
| [10] | DUMUX. http://www.dumux.org/. |
| [11] | DUNE. http://www.dune-project.org/. |
| [12] | Olaf Ippisch and Markus Blatt. Scalability of μφ and the parallel algebraic multigrid solver in dune-istl. In Hierarchical Methods for Dynamics in Complex Molecular Systems, volume 10, pages 527--532. Forschungszentrum Jülich GmbH, 2012. |
| [13] | OPM. http://www.opm-project.org/. |
| [14] | PETSc. http://www.mcs.anl.gov/petsc/. |
| [15] | SPPEXA. http://www.sppexxa.de/. |
